


But first, we need to learn how to calculate the standardized score that makes up a standard normal distribution. These properties enable us to use the normal distribution to understand how scores relate to one another within and across a distribution.
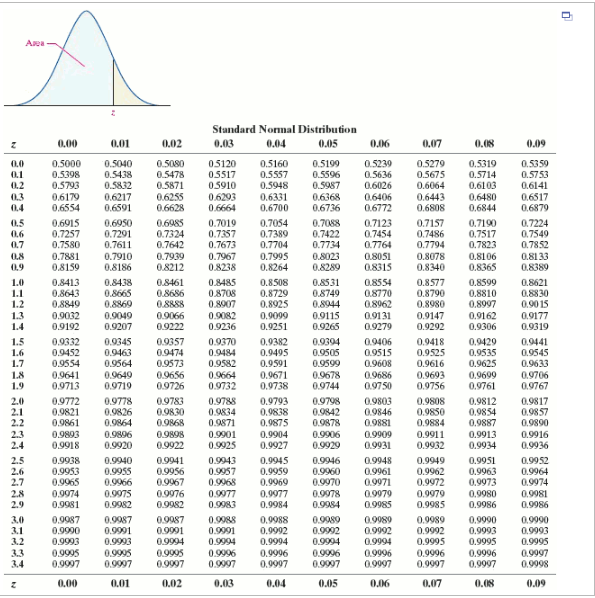
68% of the area of a normal distribution is within one standard deviation of the mean.Normal distributions are defined by two parameters, the mean ( ) and the standard deviation ( s).Normal distributions are denser in the center and less dense in the tails.The area under the normal curve is equal to 1.0.The mean, median, and mode of a normal distribution are equal.Normal distributions are symmetric around their mean.Seven features of normal distributions are listed below. We will focus on the standard normal distribution (also known as the unit normal distribution), which has a mean of 0 and a standard deviation of 1 (i.e., the red distribution in Figure 4.1). What is consistent about all normal distribution is the shape and the proportion of scores within a given distance along the x-axis. These as well as all other normal distributions are symmetric with relatively more values at the center of the distribution and relatively few in the tails.
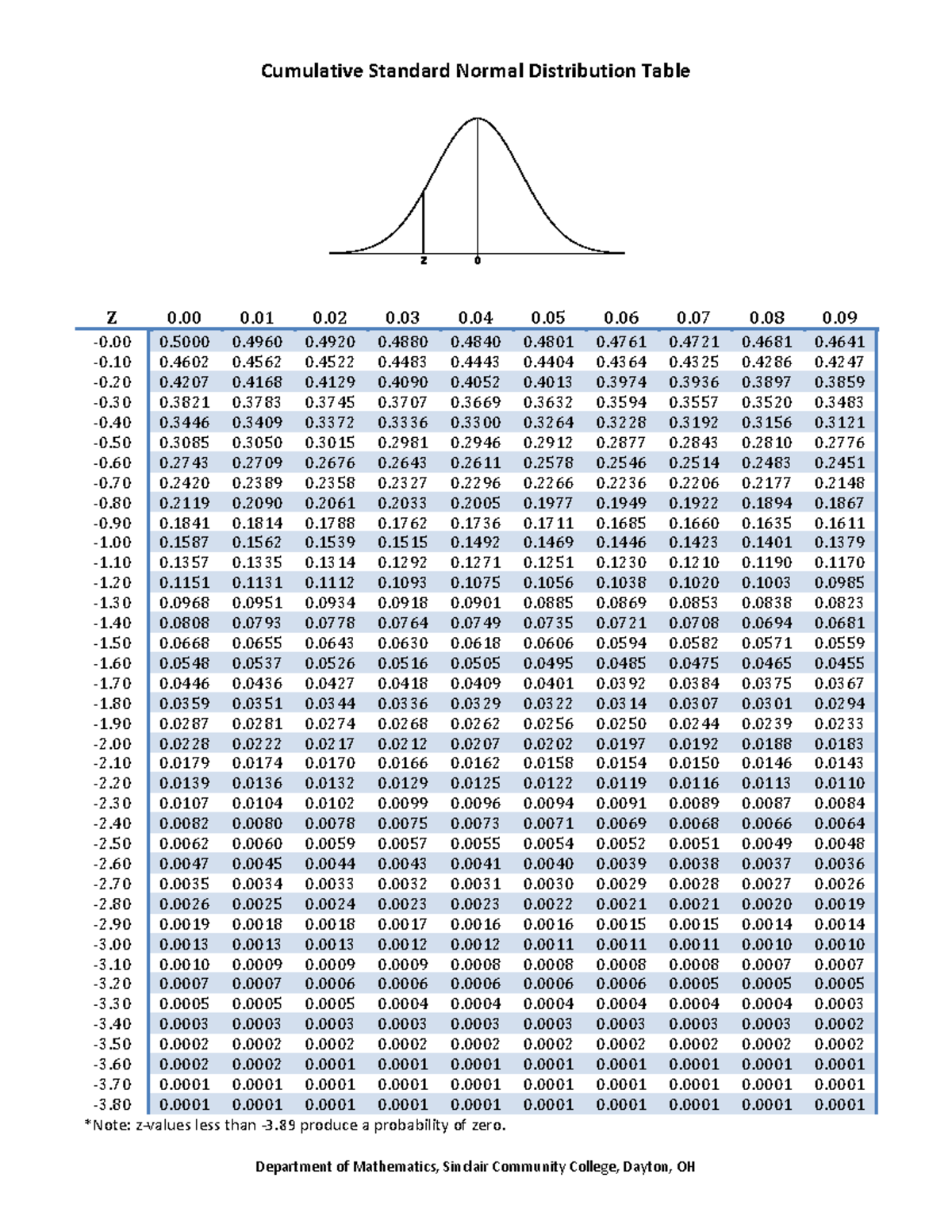
The blue (left-most) distribution has a mean of −3 and a standard deviation of 0.5, the distribution in red (the middle distribution) has a mean of 0 and a standard deviation of 1, and the black (right-most) distribution has a mean of 2 and a standard deviation of 3. Figure 4.1 shows three normal distributions. Normal distributions can differ in their means and in their standard deviations. Strictly speaking, it is not correct to talk about “the normal distribution” since there are many normal distributions. It is also called the “Gaussian curve” of Gaussian distribution after the mathematician Karl Friedrich Gauss. It is sometimes called the “bell curve,” although the tonal qualities of such a bell would be less than pleasing. The normal distribution is the most important and most widely used distribution in statistics. Moving forward, we now turn our attention to how scores within a distribution are related to one another, how to precisely describe a score’s location within the distribution, and how to compare scores from different distributions. These simple tools, and the principles behind them, will help you interpret information presented to you and understand the basics of a variable. We now understand how to describe and present our data visually and numerically.


 0 kommentar(er)
0 kommentar(er)
